专栏原创出处:github-源笔记文件 (opens new window) ,github-源码 (opens new window),欢迎 Star,转载请附上原文出处链接和本声明。
# 1. 树的概念
具有 个节点的有限集称为树。
当 时称为空树;
当 时,仅有一个特定的称为根的结点,其余结点可分为 个互不相交的有限集。每一个集合本身又是一棵树,称为根的子树。
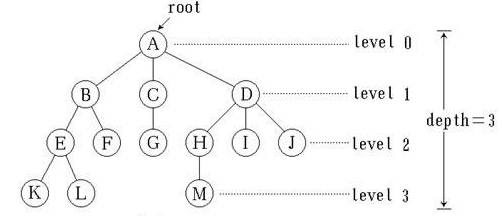
特点:树是非线性结构,数据元素具有"一对多"的逻辑关系;树中的每个元素最多有一个前驱结点,有多个后继结点。
# 2. 二叉树
二叉树是一种更为典型的树树状结构。如它名字所描述的那样,二叉树是每个节点最多有两个子树的树结构,通常子树被称作“左子树”和“右子树”。
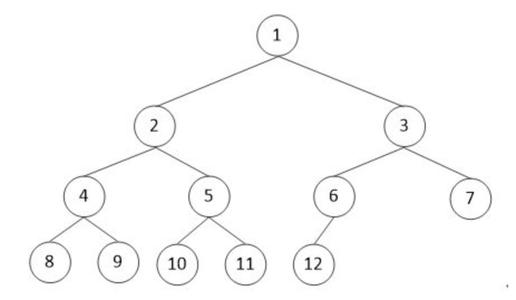
二叉树示例图
# 2.1 二叉树的遍历
- 前序遍历:首先访问根节点,然后遍历左子树,最后遍历右子树。
- 中序遍历:先遍历左子树,然后访问根节点,然后遍历右子树。
- 后序遍历:先遍历左子树,然后遍历右子树,最后访问树的根节点。
- 层级遍历:逐层遍历,二叉树的最大深度也就是层级树。
对于上述三种遍历,我们简化为,前中后只是表明遍历时「根节点的位置」,不管根在哪儿都是从左向右。每次遍历到节点时把它看做时一棵新树按刚刚的方式继续遍历。
我们可以简化为一个不需要记忆的方法:
- 前序遍历:根 左 右
- 中序遍历:左 根 右
- 后序遍历:左 右 根
常见算法题:
前序遍历、中序遍历、后序遍历、层级遍历、计算二叉树的最大深度。
从前序与中序遍历序列构造二叉树、从中序与后序遍历序列构造二叉树、二叉树的最近公共祖先
# 2.2 二叉树的类型
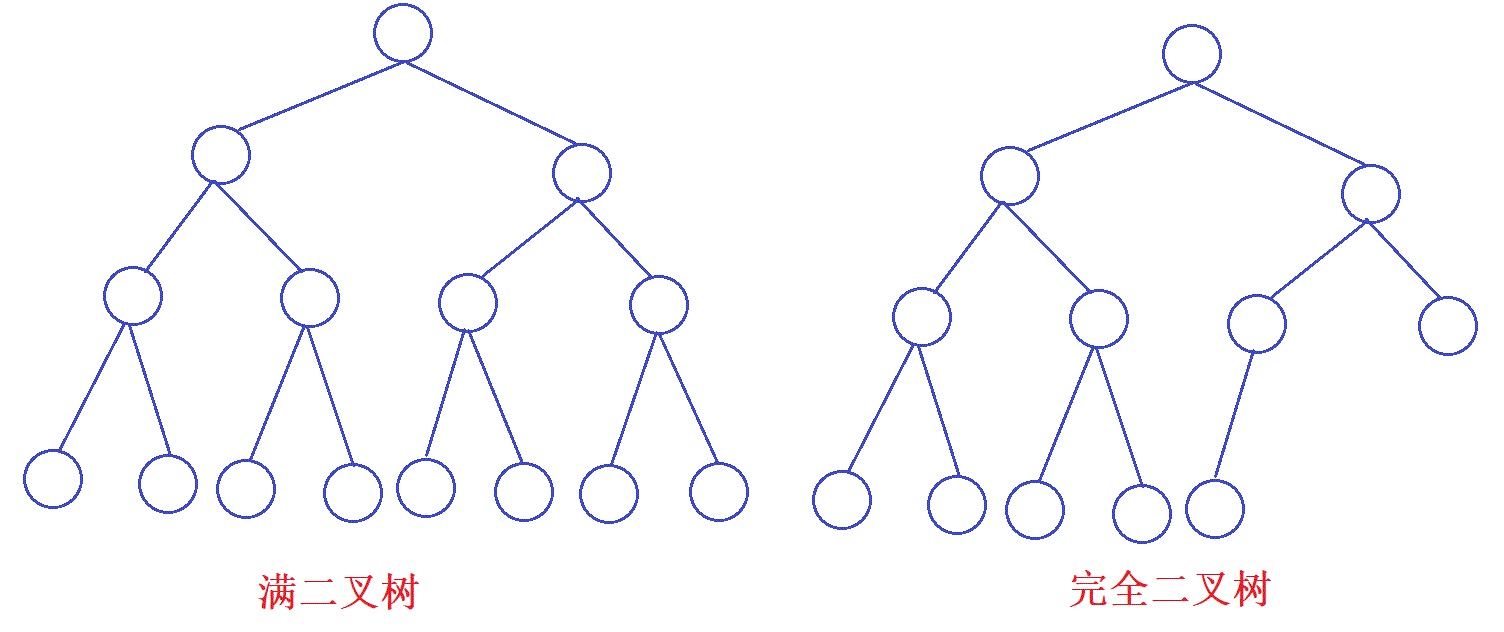
满二叉树:又叫完美二叉树,除叶子节点所有子节点都有左右子节点。
完全二叉树:除叶子节点所有子节点都有左右子节点。
# 二叉树相关算法
推荐 力扣-卡片-二叉树 (opens new window)
# 参考
本内容随着对数据结构算法的深入,持续更新。
更多相关专栏内容汇总:
