# 队列
只能在表的一端进行插入,另一端进行删除,且具有先进先出原则的线性表称为队列。
- 进行删除的一端称为队头。
- 进行插入的一端称为队尾。
- 先进先出原则:先入队的元素在队头,后入队的元素在队尾。
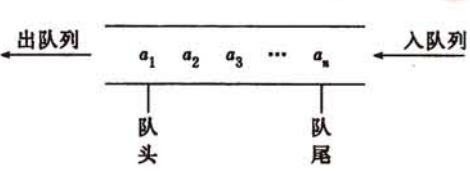
若用 表示队列,则:
- 称为队头元素;
- 称为队尾元素;
- 没有元素的队列称为空队列。
队列常见的两种操作:
- 入队:插入数据到队尾。
- 出队:删除队头第一个元素。
限定插入和删除操作在表的两端进行的线性表称为双端队列。

双端队列又可以分为:
- 输出受限的双端队列:一个端点只允许插入和删除,另一个端点只允许插入。
- 输入受限的双端队列:一个端点只允许插入和删除,另一个端点只允许删除。
- 双端队列也可以退化成栈,即只能在一端进行插入和删除。
# 队列基本操作
- 向队尾添加元素(入队)
- 删除队首元素(出队)
- 获取队首的元素值(存取)
- 判断队列是否为满
- 判断队列是否为空
# 顺序队列
用顺序存储方式存储的队列称为顺序队列。
元素入队只需将元素添加到队列的最后一个位置即可,但元素出队时队头元素的位置如何变化?
- 元素出队后,只需将下一个元素设置成新队头。
优点:队列中其他元素地址无需改变;
缺点:随着元素不断出队,队头位置后移,可能出现存储空间不足的情况,从而导致新元素无法入队;同时队头前端存在大量空闲存储空间,造成空间的浪费。 - 队头元素必须存放在存储空间的第一个位置,元素出队后,所有元素向前移动一个位置。
优点:有效的利用了存储空间; 缺点:所有元素存储位置都要改变,时间效率低。
出于空间、时间效率考虑,暂时采用牺牲空间换取时间的方式,采用方式 1 来设置队头 。
队列指针的设置及队空判断:
- 设 为队头指针,指示队头元素在顺序队列中的位置;
- 设 为队尾指针,指示队尾元素的下一个位置,初始化时指向队头:;
- 用 表示队列的存储空间大小;
- 当 时队空,当 时队列溢出,不能再添加元素。
# 顺序队列的初始化
- 申请容量为 的存储空间, 指向空间的基地址;
- 设 。
# 顺序队列的入队
- 判断队列是否溢出,若溢出不能添加元素;
- 否则将新元素入队,队尾指针加 1:。
# 顺序队列之出队
- 判断队列是否为空,若队空则不能删除元素;
- 否则队头元素出队,队头指针加 1:。
# 循环队列
将队头与队尾连接形成闭环的队列称为循环队列。
- 元素出队:队头指针顺时针移动一个位置;
- 元素入队:队尾指针顺时针移动一个位置。
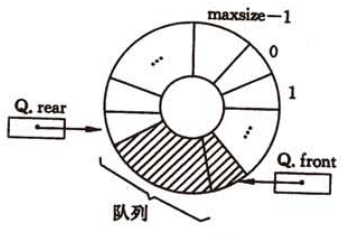
循环队列队满时便不能再添加新的元素,若 和 指针的定义与顺序队列中相同,则出现 时无法判断队列是满还是空的情况,所以如何判断队满呢?
- 新增变量 表示队列元素个数,当 时队满;当 时队空。
- 循环队列少用一个元素,当队头指针在队尾指针的下一个位置时,队列为满,队列元素为 个;当 时队空。
为了操作的便捷性,通常采用方式 2 判断队空队满,以下循环队列的操作以方式 2 为基准。
队空、队满、队列元素个数判断:
- 队满:;
- 队空:;
- 队列中有效元素个数:。
# 循环队列的初始化
- 申请容量为 的存储空间, 指向空间的基地址。
- 设 。
# 循环队列的入队
- 判断循环队列是否队满,若队满则不能添加新元素
- 否则将新元素入队,队尾指针加 1:
# 循环队列之出队
- 判断队列是否为空,若队空则不能再删除元素
- 否则队头元素出队,队头指针加 1:
# 链式队列
用链接存储方式实现的队列称为链式队列。
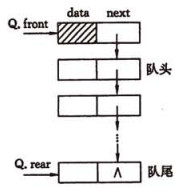
链式队列的指针:
- 队头指针: 始终指向头结点
- 队尾指针: 指向队尾结点,初始化时 指向头结点
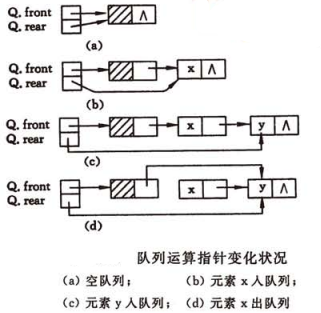
# 链式队列的初始化
- 创建一个新结点作为链式队列的头结点,并将队头和队尾指针指向头结点
- 头结点的指针域设为
# 链式队列的入队
将元素插入到队尾:
- 创建指针域为 的新结点
- 将新结点插入到队尾结点之后,修改队尾结点指针域:
- 修改队尾指针:
# 链式队列之出队
删除链表的首元结点:
- 判断队列是否为空,若为空则不能删除结点
- 否则获取首元结点 的数据域
- 删除首元结点,队头指针指向下一个结点:
- 元素出队后再次判断队列是否为空,若为空将队尾指针指向头结点:
- 释放结点
# 循环队列和链式队列的比较
时间复杂度:循环队列和链式队列入队、出队的时间复杂度都为
空间上复杂度:
- 循环队列初始化时必须申请存储空间,队列的有效长度受限,在操作过程中队列的有效元素个数小于存储空间大小,造成空间浪费。
- 链式队列存储过程中需要一个指针域,会产生空间上的开销,但队列元素个数不会受限制。
# 顺序队列与链式队列的比较
顺序队列有固定的存储空间,不适用于存储空间很大,删除插入很频繁的操作,此时顺序队列的空间利用率很低;反之,链式队列适用此情况。
顺序队列的访问简单,对队列内部元素的访问便捷;链式队列元素需便利整个链表。
# 应用实例
应用场景:双端队列最常用的地方就是实现一个长度动态变化的窗口或者连续区间,而动态窗口这种数据结构在很多题目里都有运用。
- 银行拿号排队问题
# 算法例题
1.滑动窗口最大值
例题:给定一个数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口 k 内的数字,滑动窗口每次只向右移动一位。返回滑动窗口最大值。
说明:可以假设 k 总是有效的,1 ≤ k ≤ 输入数组的大小,且输入数组不为空。
示例:给定一个数组以及一个窗口的长度 k,现在移动这个窗口,要求打印出一个数组,数组里的每个元素是当前窗口当中最大的那个数。
输入:nums = [1, 3, -1, -3, 5, 3, 6, 7],k = 3
输出:[3, 3, 5, 5, 6, 7]
解题思路: 思路 1:移动窗口,扫描,获得最大值。假设数组里有 n 个元素,算法复杂度就是 。这是最直观的做法。
思路 2:利用一个双端队列来保存当前窗口中最大那个数在数组里的下标,双端队列新的头就是当前窗口中最大的那个数。通过该下标,可以很快地知道新的窗口是否仍包含原来那个最大的数。如果不再包含,我们就把旧的数从双端队列的头删除。
因为双端队列能让上面的这两种操作都能在 O(1) 的时间里完成,所以整个算法的复杂度能控制在 。

- 初始化窗口 k=3,包含 1,3,-1,把 1 的下标压入双端队列的尾部;
- 把 3 和双端队列的队尾的数据逐个比较,3 >1,把 1 的下标弹出,把 3 的下标压入队尾;
- -1<3,-1 压入双端队列队尾保留到下一窗口进行比较;
- 3 为当前窗口的最大值;
- 窗口移动,-3 与队尾数据逐个比较,-3<-1,-3 压入双端队列队尾保留;
- 3 为当前窗口的最大值;
- 窗口继续移动,5>-3,-3 从双端队列队尾弹出;
- 5>-1,-1 从队尾弹出;
- 3 超出当前窗口,从队列头部弹出;
- 5 压入队列头部,成为当前窗口最大值;
- 继续移动窗口,操作与上述同理。
窗口最大值只需读取双端队列头部元素。
# 参考
- 《数据结构(C语言版)》 严魏敏、吴伟民著
- 《数据结构(第3版)》 刘大有等著
- 《搞定数据结构与算法》 苏勇